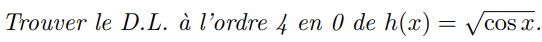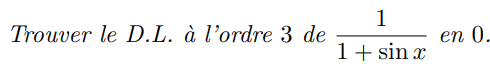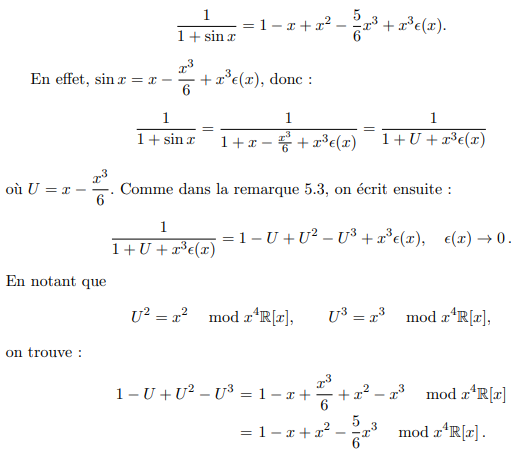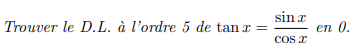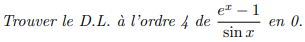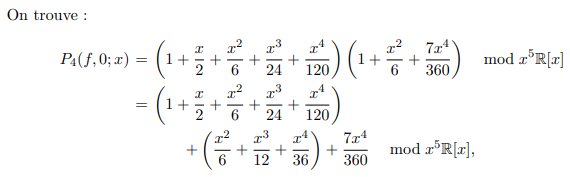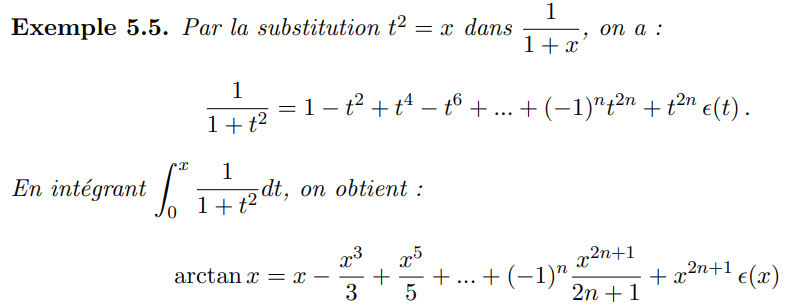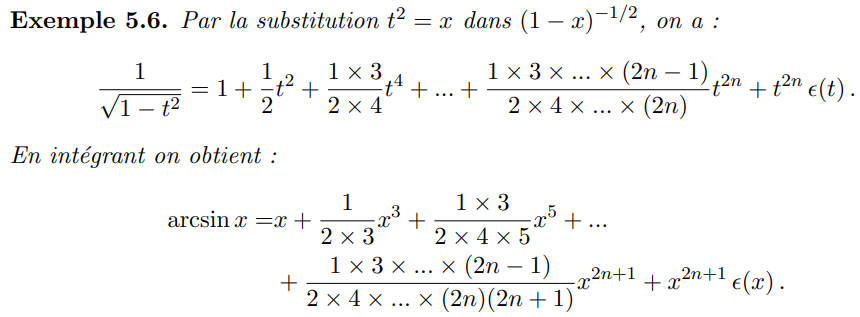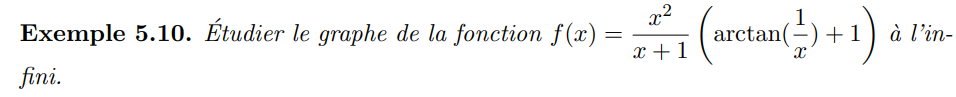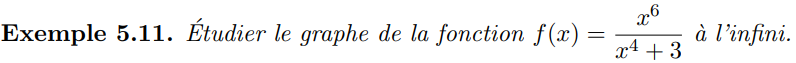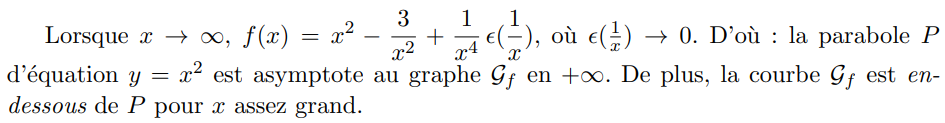Développement limité

Définition

Soient $I=]\alpha,\beta[\subset\Bbb R$, $a\in I$ et $f:I\to\Bbb R$ définie sur $I$ sauf éventuellement en $a$ et soit $n\in\Bbb N$
On dit que la fonction $f$ a un développement limité en $a$ à l'ordre $n$ s'il existe une fonction $\varepsilon(x)$ sur $I$ et des coefficients $c_0,c_1,\ldots,c_n$ tq $$f(x)={{\sum^n_{k=0}\left(c_k(x-a)^k\right)+(x-a)^n\epsilon(x)}}$$ pour tout $x\in I\setminus\{a\}$ et que $\underset{x\to a}\lim\varepsilon(x)=0$

(Négligeabilité - Petitot)

Toute fonction $f\in\mathcal C^n(I,\Bbb R)$ admet un développement limité en $a\in I$ à l'ordre $n$ avec $${{c_k}}={{\frac{f^k(a)}{k!} }}\text{ pour }k={{0,\ldots,n}}$$

Ordre

Remarque :
Si $f$ admet un développement limité en $a$ à l'ordre $n$, alors $f$ admet un développement limité en $a$ à tout ordre $k\leqslant n$

Remarque :
Si $f$ admet un développement limité en $a$ à l'ordre $n$, alors soit $f$ est définie et continue en $a$, soit elle est prolongeable par continuité en $a$

(Continuité, Prolongement par continuité)

Calcul du développement limité

Développement limités usuels en 0

Arcsinus (Développement limité en 0)
Arctangente (Développement limité en 0)
Cosinus (Développement limité en 0)
Fonction exponentielle (Développement limité en 0)
Fonction inverse (Développement limité en 0)
Fonction tangente (Développement limité en 0)
Logarithme népérien - Logarithme naturel (Développement limité en 0)
Puissance (Développement limité en 0)
Sinus (Développement limité en 0)

Les développements limités usuels s'obtiennent en utilisant la formule de Taylor-Young avec $a=0$

Les formules de DL usuels ne peuvent être utilisés qu'au voisinage de $0$, donc il faut faire attention aux changements de variable

Combinaison linéaire

Proposition :
Soient $f$ et $g$ des fonctions ayant un développement limité d'ordre $n$ en $a\in]\alpha,\beta[$ et soit $(\lambda,\mu)\in\Bbb R^2$ $${{P_n(\lambda f+\mu g,a,x)}}={{\lambda P_n(f,a,x)+\mu P_n(g,a,x)}}$$

Multiplication

Proposition :
Soient $f$ et $g$ des fonctions ayant un développement limité d'ordre $n$ en $a\in]\alpha,\beta[$ et soit $(\lambda,\mu)\in\Bbb R^2$
$${{P_n(fg,a,x)}}={{P_n(f,a,x)P_n(g,a,x)+(x-a)^{n+1}R(x)}}$$

Division

Proposition :
Soient $f$ et $g$ des fonctions ayant un développement limité d'ordre $n$ en $a\in]\alpha,\beta[$ et soit $(\lambda,\mu)\in\Bbb R^2$
$${{P_n\left(\frac fg,a,x\right)}}={{P_n(f,a,x)P_n\left(\frac1g,a,x\right)+(x-a)^{n+1}R(x)}}$$

Composition

Proposition :
Soient $f:]\alpha,\beta[\to]\gamma,\delta[$ et $g:]\gamma,\delta[\to\Bbb R$ des fonctions ayant un DL d'ordre $n$ respectivement en $a\in]\alpha,\beta[$ et $b\in]\gamma,\delta[$ avec $b={{f(a)}}$
Alors la fonction composée $g\circ f(x)$ admet un DL d'ordre $n$ en $a$ dont la partie polynomiale $P_n(g\circ f,a,x)$ s'obtient en ne conservant dans la composée $P_n(g,b,P_n(f,a,x))$ que les monômes $(x-a)^k$ de degré $k\leqslant n$, i.e. : $${{P_n(g\circ f,a,x)}}={{P_n(g,b,P_n(f,a,x))\mod(x-a)^{n+1}\Bbb R[x]}}$$

(Composition)

Démonstration :

Intégration

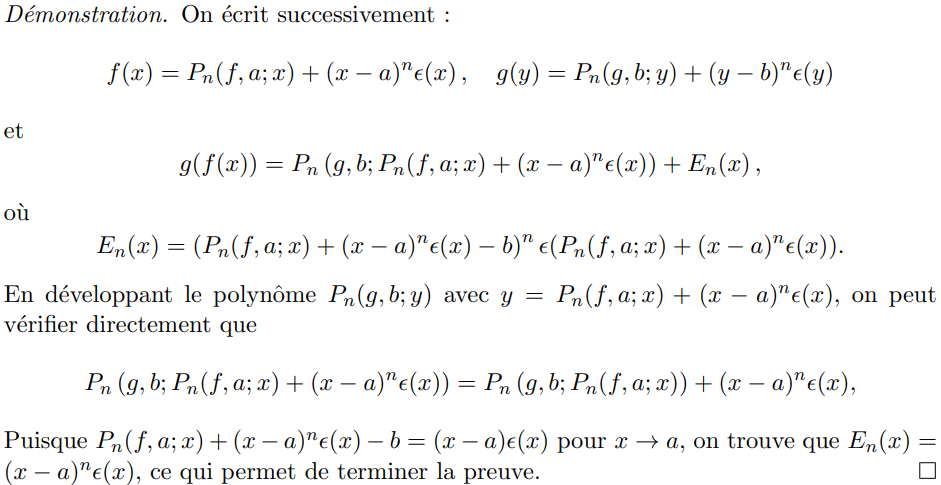
Proposition :
Si $f$ est une fonction continue sur $]\alpha,\beta[$ qui admet un DL d'ordre $n$ en $a\in]\alpha,\beta[$ , alors toute primitive $F$ de $f$ sur $]\alpha,\beta[$ admet un DL d'ordre $n+1$ en $a$, avec $${{P_{n+1}(F,a,x)}}={{F(a)+\int^x_aP_n(f,a,t)dt}}$$

(Primitive, Intégrale - Intégration)

Démonstration :

Formules pour les fonctions de deux variables

Formule du développement limité à l'ordre $2$ en $(x_0,y_0)$ pour une fonction de deux variables : $$\begin{align} {{f(x_0+h,y_0+k)}}=\,&{{f(x_0,y_0)}}\\ &+{{h\frac{\partial f}{\partial x}(x_0,y_0)+k\frac{\partial f}{\partial y}(x_0,y_0)}}\\ &+{{\frac12\left[ h^2\frac{\partial^2f}{\partial x^2}(x_0,y_0)+2hk\frac{\partial^2f}{\partial x\partial y}(x_0,y_0)+k^2\frac{\partial^2f}{\partial y^2}(x_0,y_0)\right]}}\\ &+{{o(\lVert(h,k)\rVert^2)}}\end{align}$$

Formule du développement limité à l'ordre $2$ pour une fonction $f:{\Bbb R}^n\to{\Bbb R}$ de classe $\mathscr C^2$ : $${{f(x_0+h)}}={{f(x_0)}}+{{J_f(x_0)h}}+{{\frac12 h^T\cdot H_f(x_0)\cdot h}}+{{o(\lVert h\rVert^2)}}$$

(Dérivée partielle, Dérivée partielle seconde, Matrice jacobienne - Jacobienne, Matrice Hessienne, Matrice transposée, Négligeabilité - Petitot)

Fonctions particulières

Proposition :
Supposons que $f$ admet un développement limité en $a$ à l'ordre $n$
1. $n\geqslant1$ $\Rightarrow$ $f$ est dérivable en $a$ et ${{f(a)}}={{c_0}}$, ${{f'(a)}}={{c_1}}$
2. Les coefficients $c_0,c_1,\ldots,c_n$ sont uniquement déterminés
3. $f$ paire $\Rightarrow$ les coefficients $c_{2k+1}$ sont nuls en $a=0$
4. $f$ impaire $\Rightarrow$ les coefficients $c_{2k}$ sont nuls en $a=0$

(Dérivabilité, Fonction paire, Fonction impaire)

Démonstration :

Lien avec le gradient

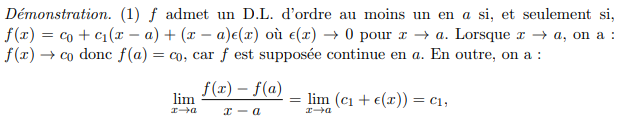
Soient $M_0=(x_0,y_0,z_0)\in\Omega\subset\Bbb R^3$ et $(h,k,l)\in\Bbb R^3$ tq $M=(x_0+h,y_0+k,z_0+l)\in\Omega$
Si on $\overrightarrow{\Delta M}=h\vec i+k\vec j+l\vec k$, alors $M=M_0+\overrightarrow{\Delta M}$
La partie linéaire du développement limité de $f$ à l'ordre $1$ en $M_0$ peut s'écrire $$\overrightarrow{\operatorname{grad}(f)}_{M_0}\cdot\overrightarrow{\Delta M}$$
Et le développement linéaire à l'ordre $1$ de $f$ en $M_0$ s'écrit : $$f(M)=f(M_0)+\overrightarrow{\operatorname{grad}(f)}_{M_0}\cdot\overrightarrow{\Delta M}+\lVert\overrightarrow{\Delta M}\rVert\varepsilon(\overrightarrow{\Delta M})$$

(Gradient)

Développement limité

Applications

Limite
Tangente (géométrie)
Courbe - Courbe paramétrée
Série convergente, Intégrale impropre - Intégrale généralisée

Branches infinies

L'étude de branches infinies peut se faire via le DL avec le changement de variable $x\mapsto t=\frac1x$

(Développement limité, Changement de variable)